third and final installment of the "triptych" of September dedicated to the study of the allocation of the shares.
After the first section on the allocation of shares from a frequentist point of view
http://acandio.blogspot.com/2010/09/hattrick-il-random-nellassegnazione.html
where we saw that
After the first section on the allocation of shares from a frequentist point of view
http://acandio.blogspot.com/2010/09/hattrick-il-random-nellassegnazione.html
where we saw that
- The total number of shares after the amendments of January 2010 is no longer fixed at 10. This means that if you know how many shares are assigned to a team, I will not know più automaticamente quante ne ha il team 2. Prima infatti era un numero fissato, facile da calcolare: se il team 1 ne aveva 8, allora il team 2 ne aveva 2 (completa dipendenza). Ora ogni team può avere da 0 a 5 delle sue azioni esclusive e da 0 a 5 di quelle comuni. Quindi se il team 1 prende tutte e 5 le azioni comuni, il team 2 al massimo potrà ottenere tutte le sue esclusive, per un totale di 5. Se il team 1 non prende nessuna azione comune, allora il team 2 può ottenere da 5 (dato che prende tutte le comuni) a 10 (se riesce a ottenere anche tutte le esclusive). C'è quindi una relazione tra le azioni del team 1 e quelle del team 2, ma non più di completa dipendenza, ora è solo una dipendenza parziale.
- Questo fact that makes it possible pairs of values \u200b\u200bof the shares of the two teams are no longer only 11, ie 10 to 0 in the first and second, 9 to 1 on the first and second and so on ... but there are now 91 possible combinations. The curve of distribution is no longer in steps, but it is much sweeter and closer to the fair value of the allotment of shares.
and a second part with setting probability
http://acandio.blogspot.com/2010/09/hattrick-il-random-nellassegnazione_21.html where
http://acandio.blogspot.com/2010/09/hattrick-il-random-nellassegnazione_21.html where
- was traced in the above more formal way, highlighting how it went from the allotment of shares premodifiche such
to one after the changes, like this:
and as I said, just do the sum of the diagonals and you see what is the% of have 5 shares, to have 6, etc. ... (See the image diagonal of 15 shares)

So, as summarized effectively Laiho-NH, "Before you had 10 more shares. Now you have 10 shares on average, because for every game where there are 15, there is a probabilistically with 5, 14 for each match there is one with 6 and so on ... "
The number of shares expected to cool team does not change, but very much behind the scenes. "
The number of shares expected to cool team does not change, but very much behind the scenes. "
****
CHANGES PRE
Now we continue on this path and insert it into account offense and defense. Start by
CHANGES PRE which is simpler.
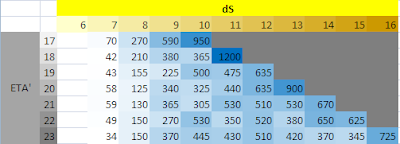
assume that a team is of a level stronger than 2 team in each division (DC and in each attack and each defense), here is the table where you see opposing units in the first team (in blue font) with those Team 2 (in brown). The chance to score is 63.53% for team 1 and 36.47% for the second team, using the known formula developed by GM-Homerjay: TASK1 ^ 3.6 / (3.6 + diF1 TASK1 ^ ^ 3.6)
CHANGES PRE which is simpler.
assume that a team is of a level stronger than 2 team in each division (DC and in each attack and each defense), here is the table where you see opposing units in the first team (in blue font) with those Team 2 (in brown). The chance to score is 63.53% for team 1 and 36.47% for the second team, using the known formula developed by GM-Homerjay: TASK1 ^ 3.6 / (3.6 + diF1 TASK1 ^ ^ 3.6)

does not complicate the analysis by including and comparing tactics, rest in a normal healthy with a probability of scoring total of the weighted average of the individual, that all are equal is equal to the value of the individual themselves.
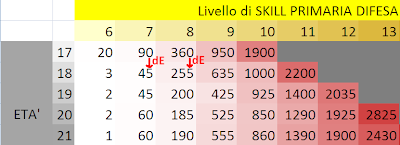
So far all we have, we now apply these values \u200b\u200bto each probabilistic action pending in Tables 1 and 2, as seen above.
For example, consider the case "four actions assigned to team 1" and "6 actions assigned to team 2" in Table 1. I see that this event has the 8, 20% chance of success.
If it happens there are 4 actions for team 1, with 63.53% chance of being achieved, then 4 * 0.6353 = 2.54 expected goals for the team 1. There are 6 actions for the team 2, 6 * 0.3647 = 2.19 expected goals for the team 2.
From a formal point of view the expected number of goals is equal to the expected number of shares multiplied by the weighted average score of the probability of each action.
So far all we have, we now apply these values \u200b\u200bto each probabilistic action pending in Tables 1 and 2, as seen above.
For example, consider the case "four actions assigned to team 1" and "6 actions assigned to team 2" in Table 1. I see that this event has the 8, 20% chance of success.
If it happens there are 4 actions for team 1, with 63.53% chance of being achieved, then 4 * 0.6353 = 2.54 expected goals for the team 1. There are 6 actions for the team 2, 6 * 0.3647 = 2.19 expected goals for the team 2.
From a formal point of view the expected number of goals is equal to the expected number of shares multiplied by the weighted average score of the probability of each action.
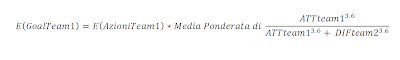 We are now in the hands of these values: 2.54 goals expected for a team, 2.19 expected goals for the team 2.
We are now in the hands of these values: 2.54 goals expected for a team, 2.19 expected goals for the team 2. Well, but how many goals are 2:54? 3 or 2? or rather, how many times are 3 and 2? If
are expected, are a likely outcome, I can only imagine them as means of a Gaussian distribution and group the distribution values \u200b\u200bto integers.
A chart can better represent the concept:

You see I made a 2:54 Gaussian with mean and standard deviation 0.60 (then the change, meanwhile, imposed this issue). Gather all probability from 1.50 to 2.50 and check the "2 goals, grouped from 2.50 to 3.50 and check out to" third goal "and so on.
The most observant of you may have already noticed two problems: the first is not feasible five goals, one team has only four actions available, and the second is that the Gaussian has values \u200b\u200b(albeit minimal), even lower than - 0.5 and above the maximum possible value of shares + 0.5 ... then there I just have to redistribute these probabilities residual between the previous ones (simply multiply by 1 divided by the sum of the probabilities really attainable, a table will illustrate this point later).
Do the same for the team 2. Gaussian even for him, and gather data for him. We will then
Gaussian and we can easily see two possible outcomes.
Now we see in the table is clear:

first calculates the values \u200b\u200bof the goals expected from the formula above and put in the right part of the table. After which they are excluded (gray area) the probability achievable. It is therefore the sum of those achievable and we get the right values \u200b\u200bthat are 99.95% for the first team (remember the exclusion of the probability of those "five goals") and 100% for team 2.
We then multiply the values \u200b\u200bfor the first team to 1/99.95%, and the correct values \u200b\u200bin the table on the left.
And so a team will be able to do with his fourth goal in the shares granted
0 0.03% of the cases indicates that P (0; team1)
1 goal in 4.10% of the cases indicates that P (1; team1)
2 goals in the 43.16% of the cases indicates that P (2; team1)
3 goals in the 47.26% of the cases indicates that P (3; team1)
4 goals in 5.45% of the cases indicates that P (4; team1 )
the which gives the desired distribution with mean equal to 2:54 of goals and desired standard deviation 0.60
Same thing for the team 2.
At this point we have the chances of goals scored for each team.
Since they are independent events we can provide considering the joint probability.
So the probability of a tie for second at 2 is 43.13% * 57.26% = 24.69%.
had one for 3 to 3 is 47.26% * 28.73% = 13:57%. And so on.
So the probability of a draw P ("X") is the sum of the probability of having one of the possible draws, and then the sum of the probabilities of 0 and 0, 1 to 1 of 2 in 2, 3 to 3, 4 to 4.
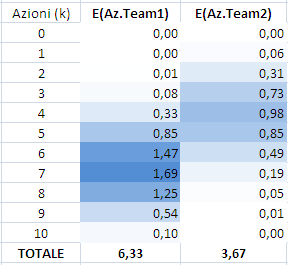
 per calcolare la Probabilità di vittoria del team 1 P("1") mi basta moltiplicare le probabilità di tutti i risultati che la possano dare e quindi 1 a 0, 2 a 0, 2 a 1, 3 a 0, 3 a 1, 3 a 2, 4 a 0, 4 a 1, 4 a 2, 4 a 3. Le sommo e il gioco è fatto.
per calcolare la Probabilità di vittoria del team 1 P("1") mi basta moltiplicare le probabilità di tutti i risultati che la possano dare e quindi 1 a 0, 2 a 0, 2 a 1, 3 a 0, 3 a 1, 3 a 2, 4 a 0, 4 a 1, 4 a 2, 4 a 3. Le sommo e il gioco è fatto. Idem per il team 2 ed ecco i valori delle somme delle probabilità di avere "1/X/2" evidenziate in rosso nella tabella (ho tagliato la parte destra per semplicità)
 Quindi con 4 azioni al team 1 e 6 al team 2 e i valori dati di centrocampi, attacchi e difese mi aspetto il 43.80% di vittorie per il team 1, il 38.87% di pareggi e il 17.32% di vittorie per il team 2.
Quindi con 4 azioni al team 1 e 6 al team 2 e i valori dati di centrocampi, attacchi e difese mi aspetto il 43.80% di vittorie per il team 1, il 38.87% di pareggi e il 17.32% di vittorie per il team 2. In summary
 These are the values \u200b\u200bof this event. The pair of actions assigned (4, 6) occurs in 20.8% of cases, the expected goals with 2:54 and 2.19 for the first team for the second team translates into just under 44% of wins for a team, just under 39% draws and 17% of wins for team 2. Having these values \u200b\u200b
These are the values \u200b\u200bof this event. The pair of actions assigned (4, 6) occurs in 20.8% of cases, the expected goals with 2:54 and 2.19 for the first team for the second team translates into just under 44% of wins for a team, just under 39% draws and 17% of wins for team 2. Having these values \u200b\u200b1/X/2 .20% in 8 cases, this means that this event contributes to the total 43.80% * 8.20% = 3:59% to win by 1, to 38.87% * 8.20% = 3.18% of draws and * 8:20 to 17:32% to 2% of wins in total.
As shown in the table:

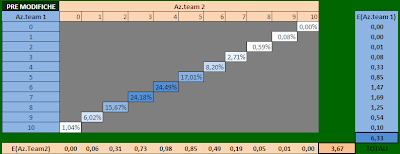
At this point, simply repeat the procedure per tutti gli eventi e otteniamo la tabelle:

e

non mi resta che sommare le celle che contengono i valori di 1/X/2 Totali per ottenere il valore finale che cercavo:

quindi, in conclusione, prima delle modifiche con quei valori mi potevo aspettare quasi l'89% di vittorie per il team 1, il 7% di pareggi e poco meno del 4% di vittorie per il team 2.
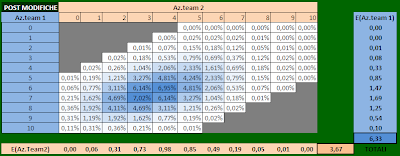
POST MODIFICHE
Dopo le modifiche i casi passano da 11 a 91 e le cose si complicano un pochino.
Niente di impossibile comunque.
I proceeded to consider separately the data column by column, starting from the right, ie "10 actions assigned to team 2" and seeing what the results are expected for all other possible actions of the team variandi 1 (in this case 10 having the team 2, team 1 will have a variable number from 0 to 5), and then proceed to all other columns to the left.
The analysis is broken down into 10 phases.
For example, in the fourth column from the right we find the values \u200b\u200bseen in the example above (4 to team 1, team 6 to 2):
Niente di impossibile comunque.
I proceeded to consider separately the data column by column, starting from the right, ie "10 actions assigned to team 2" and seeing what the results are expected for all other possible actions of the team variandi 1 (in this case 10 having the team 2, team 1 will have a variable number from 0 to 5), and then proceed to all other columns to the left.
The analysis is broken down into 10 phases.
For example, in the fourth column from the right we find the values \u200b\u200bseen in the example above (4 to team 1, team 6 to 2):

grouping the 10 columns in one table we get the table of actions and goals expected:

and the expected results, obtained as above by assessing the likelihood of 1/X/2 for each event and then multiplied by the probability of the event.

aggregating the various phases obtained separately into the fixed number of shares for the team 2 gives the total is 90.97% of 1, 6.40% and 2.62% of X 2.
At this point a comparison can be established before and after the change:
At this point a comparison can be established before and after the change:

with a standard deviation of the Gaussian 0.6 goals expected that the changes we see in this case, increase the% of win the strongest team, reduce ties and reduce even more the results "unexpected", that the victories of the two weakest teams: a reduction of 1.31%, -33.3% to 3.93% of the previous results "2", which were obtained previously.
If you mean the "random" as the% of the results "unexpected" that favor the weakest team, well in that case, the numbers tell us that the "random" is (and there should be), but was reduced .
Some may ask whether this conclusion depends on the assumed standard deviation (which is the only discretionary element in all this analysis), well then let us look at 0.4 and 0.8 instead of 0.6 and we see that
If you mean the "random" as the% of the results "unexpected" that favor the weakest team, well in that case, the numbers tell us that the "random" is (and there should be), but was reduced .
Some may ask whether this conclusion depends on the assumed standard deviation (which is the only discretionary element in all this analysis), well then let us look at 0.4 and 0.8 instead of 0.6 and we see that

cambiano i valori relativi, ma pochissimo quelli assoluti (i "2" si risudono del 1.33% con dev.st 0.4, del 1.31% con dev.st 0.6 e del 1.32% con dev.st 0.8).
Naturalmente posso provare a impostare (e lo potete fare anche voi nel file allegato) dei valori di prova, per vedere come varino le probabilità di 1/X/2 tra PRIMA e DOPO le modifiche al variare delle valutazioni di campo.
1) Pongo tutti i reparti uguali dei due team, e poi faccio crescere il centrocampo del team 1:
Naturalmente posso provare a impostare (e lo potete fare anche voi nel file allegato) dei valori di prova, per vedere come varino le probabilità di 1/X/2 tra PRIMA e DOPO le modifiche al variare delle valutazioni di campo.
1) Pongo tutti i reparti uguali dei due team, e poi faccio crescere il centrocampo del team 1:

nel primo caso, di completo equilibrio, vedo che si riducono le % di probabilità di vittoria per uno dei due team (da 39.56% a 38.17%) e aumentano i pareggi, del 13.40% in termini relativi (cioé sul valore precedente)
Se aumento il CC del team 1 da 6 a 6,5 vedo che nella seconda tabellina ho ancora un aumento dei pareggi (meno rispetto al valore prededente), una sostanziale stabilità delle vittorie di 1 e una riduzione del 8.56% delle vittorie per il team più debole.
La dinamica continua all'aumentare del valore del CC del team 1. Quindi, le MODIFICHE:
Se aumento il CC del team 1 da 6 a 6,5 vedo che nella seconda tabellina ho ancora un aumento dei pareggi (meno rispetto al valore prededente), una sostanziale stabilità delle vittorie di 1 e una riduzione del 8.56% delle vittorie per il team più debole.
La dinamica continua all'aumentare del valore del CC del team 1. Quindi, le MODIFICHE:
- aumentano il numero dei pareggi in caso di partite equilibrate
- diminuiscono il numero di vittorie "impreviste" del team più debole, e più il team è debole, più si riducono le sue chance di vittoria "imprevista"
seem both elements on which agreement can be reached.
*****
Finally one may ask, "Well, we have seen what happens in terms of 1/X/2, but about the goal difference?". Yeah, one thing is a victory with three goals difference, another one with only a narrow goal.
How to do it? Simple: the point where we took the values \u200b\u200bof the goals expected for the two teams and calculate the% chance of victory by adding the probabilities of "1 to 0" with "2 to 1", the "2 0" etc. .. . hours disaggregate wins with 1 goal difference from those with 2 goals difference, etc. ... and we get a table so as to the "primacy of Changes"
How to do it? Simple: the point where we took the values \u200b\u200bof the goals expected for the two teams and calculate the% chance of victory by adding the probabilities of "1 to 0" with "2 to 1", the "2 0" etc. .. . hours disaggregate wins with 1 goal difference from those with 2 goals difference, etc. ... and we get a table so as to the "primacy of Changes"

as you see, for example, the number of wins for team 2 in the usual case (4 and 6 shares at a team shares the team 2) equal to 1.42% the total is all centered on "the victory with a goal difference", where we find a nice .27% of the occurrences. Not so, for example, for victories in a team event (7 actions to team 1 and team 3 to 2), in which case we have the fact 99.93% of wins of a team that moltipicate the probability of the event ( 24.18%) tells me that in this event are the victories of 24.16% of the total absolute event "a victory for the team", in which case the victories are made with more likely with 3 goals and 4 goal margin (9:54% and 8.14%).
What is best seen if I apply conditional formatting to cells
What is best seen if I apply conditional formatting to cells

back now to the results table total

that can also be seen in a chart with the x-axis the number of goals waste (in favor of team 1): a blue one for the team's victories, gray ties, wins in the red for the second team

If I do the exact same procedure for the post changes (or better, 10 the same procedures, since I'll have to break up the above analysis tabellona colonna per colonna) ottengo alla fine un confronto tra PRIMA e DOPO:

e cioé (i valori nuovi sono a destra, più scuri dei precedenti)

- diminuiscono i rettangoli rossi dei risultati "imprevisti" di vittoria per il team 2 più debole
- diminuiscono i pareggi
- aumentano le vittorie del team 1 più forte attorno ai valori più probabili (2, 3, 4 gol di scarto)
- diminuiscono le vittorie del team 1 più forte attorno ai valori meno probabili (1, 5, 6, 7 gol di scarto)
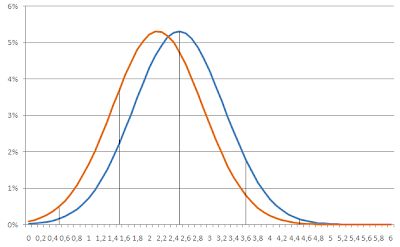
In sostanza la curva diventa più alta e più close around the most probable values, ie reduces the variance of the curve around its average .
If I represent the above graph as a trend I see in fact that the curve after modification, in red, compared to the curve of the PRE changes, in blue, is, as indicated by the arrows in the sides closer (decreasing the extreme results) and higher the maximum value:
If I represent the above graph as a trend I see in fact that the curve after modification, in red, compared to the curve of the PRE changes, in blue, is, as indicated by the arrows in the sides closer (decreasing the extreme results) and higher the maximum value:

I am attaching the file.
On the "INPUT" you can enter all the values \u200b\u200byou want and you will see:
On the "INPUT" you can enter all the values \u200b\u200byou want and you will see:
- in the green zone the estimate of the allocation of shares based on values \u200b\u200bentered
- in midfield zona viola la stima dei risultati in base ai valori di attacchi e difese inseriti (e deviazione standard), con predictor base 1/X/2 e avanzato, con l'analisi dei gol di scarto. Inoltre c'è il grafico per vedere come variano le curve relative.

QUI potete scaricarlo (sia per Excel nuovo che per versioni precedenti)
http://sites.google.com/site/andreactools/home/TOOLPredictorino1.2.xlsx?attredirects=0&d=1
Buon divertimento
Andreac-NH
edit: nota finale per i più pignoli -> se si pone tutto uguale tra team 1 e team 2 ci sono delle piccolissime differences between the% of goal difference to team 1 and team 2, which should be the same, I'm talking about hundredths of a percentage point. And I've split my head to find reasons, but after hours and hours of trial and I did not. These things are minor and completely irrelevant, but I wish it was all perfect. Be patient.
PS. take a look at ' CONTENTS of the blog, there are several items that may be of interest.
Andreace (team in Hattrick ID 1730726)
Andreace (team in Hattrick ID 1730726)
by
This work is licensed under Andreace a Creative Commons Attribution-Noncommercial 3.0 Unported License . Ie, this work may be freely copied, distributed or modified without the express permission of the author, provided that the author is clearly stated and the publication is not for commercial purposes.